Research topics
Statistical physics of soft matter
- Structure and dynamics of polymer solutions and melts in the bulk and in confinement
- Phase transitions and dynamics of single (bio-) polymer chains
- Fundamental questions in quantum mechanics and quantum field theory
- Method development in computational statistical physics
- Computer modeling of swarming behavior (non-equilibrium phase transtitions)
Computational soft matter physics
Polymer science is a highly interdisciplinary field with questions ranging from materialsscience to basic theoretical physics. Rational design of polymer-based materials needsan understanding of structure and dynamics on the molecular scale. Computersimulations of chemically realistic as well as coarse-grained models yield insight intomolecular processes and help to interpret experiments. The hierarchy of length scalesand time scales inherent in often complex molecular architectures and materialmorphologies engender the necessity for a multi-scale modeling approach. This in turn needs model as well as methods development for efficient Molecular Dynamics andMonte Carlo simulation. Even a single (bio-)macromolecule is a fascinating object initself which can exhibit phase transition-like phenomena like protein folding. The searchfor a basic statistical physical understanding of these phenomena links polymer theoryto biophysics and biology.
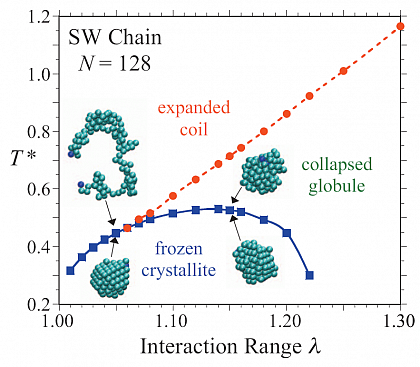
Phase transitions in a pearl-necklace chain model with square-well attraction
From a basic theoretical physics point of view, the conformational properties of linear polymers are intimately connected to path integrals or random walk theory. The methods for their analytical description link polymer theory to quantum field theory (statistical field theory) and the theory of stochastic processes. Fundamental questions in quantum field theory and a stochastic processes based understanding of quantum mechanics are interests of the group growing out of these connections.
Current Projects and Future Goals
Phase transitions of synthetic polymers
In experiments, polymer crystallization is a process where thermodynamic forces and kinetic constraints interact in a hardly controllable way. Our goal is to extend our simulation work on single chain phase transitions and to study both by simulations and by analytical theory simple models for polymer crystallization. This offers the possibility to disentangle thermodynamics and kinetics to improve our understanding of this phase transition.
Copolymers can undergo phase separation within a single molecule and variations of chain topology and chemical composition lead to a variety of microphase separated structures with always the molecular scale as the resulting length scale of the macroscopic morphology. We are studying these systems both by computer simulations and by field-theoretic methods.
Structure and dynamics in bulk and in confinement
The understanding of structure and dynamics in polymer melts is always concerned with influence of chain topology on various length and time scales. Polymers are ideal model materials for studies of the structural glass transition because many of them stay amorphous in quasi-equilibrium. But in contrast to simple liquids local mobility is an interplay of packing and local molecular architecture. On larger scales, topology leads to a polymer specific collective dynamical process termed reptation. In the vicinity of solid surfaces (e.g., confining walls or dissolved nano-particles) the structure of a polymeric liquid is perturbed leading to changes in the dynamics as well as new dynamic processes. All these phenomena are studied by means of Molecular Dynamics simulations.
Conformational and thermodynamic properties of single (bio-)molecules and their aggregates
Proteins and peptides are able of intra-molecular structure formation and often need to assume specific structures to perform their molecular function. The same interactions (e.g., hydrophobic or hydrogen bonding) generating these structures can, however, also lead to chain aggregation, e.g., amyloid formation, underlying many neuro-degenarative diseases. Understanding of the statistical mechanics and the kinetics of these competing structure formation processes can be obtained from advanced Monte Carlo simulations of specifically designed models. At the same time this yields insight into morphology generation in supramolecular chemistry.
Development of quantum mechanical simulation tools based on Nelsons stochastic mechanics
In 1966 E. Nelson derived the Schrödinger equation starting from a description of the paths of quantum particles as conservative diffusion processes. This introduces two scalar fields into the description of the properties of quantum mechanical motion. One of them is the quantum extension of the classical action, the other is the probability to find a particle at a certain space-time point. The nonlinear equations for this scalar fields (the continuity equation for the probability and the quantum mechanical extension of the Hamilton-Jacobi equation) are equivalent to the Schrödinger equation. Thus, knowing the solution of the Schrödinger equation, one can simulate the quantum mechanical paths giving the same statistics as the this solution. At the moment we are exploring the possibility of using the quantum mechanical version of Hamiltons principle (from which the equations of motion of the particles as well as the Schrödinger equation can be derived) in conjunction with the stochastic differential equations describing the particle motion, to generate solutions of the Schrödinger equation without solving it directly.
Swarming behavior within an extended Viscek model
Flocks of birds or fish show a transition from random individual motion to collective swarming behavior once their density gets high enough. A simple model capturing this behavior is the Viscek model. However, it only describes point particles without extension or further interactions. Together with colleagues at the Universidad Nacrional de La Plata in Argentina we study the behavior of an extended Viscek model we suggested, into which excluded volume and interactions can be introduced.
